Hamming score
If you have ever tried solving a Classification task using a Machine Learning (ML) algorithm, you might have come across such a term as Hamming score but never really understood it. Today that is about to change. On this page, we will:
Сover the logic behind the metric (binary, multiclass, and multi-label cases);
Check out the metric’s formula;
Find out how to interpret the Hamming score value;
Calculate the metric’s value on two examples;
And see how to work with the Hamming score using Python.
Let’s jump in.
What is the Hamming score?
The most intuitive way to evaluate the performance of any Classification algorithm is to calculate the percentage of its correct predictions. This should sound familiar to you as it is precisely the logic behind the Accuracy score. The Hamming score sticks to the same philosophy
To define the term, in Machine Learning, the Hamming score is a Classification metric featuring a fraction of the predictions that a model got right. It has the same advantages as Accuracy. The Hamming score is:
Easy to calculate;
Easy to interpret;
And a nice way to measure the model’s performance with a single value.
To evaluate a Classification model using the Hamming score, you need to have:
The ground truth classes;
And the model’s predictions.
Hamming score formula
Strictly speaking, the Hamming score does not have its own formula, just a basic logic behind the metric. Fortunately, the Hamming score and Accuracy are interchangeable for binary and multiclass cases.
So, if you have a binary or multiclass task, you can calculate the Hamming score by dividing the number of correct predictions by the total prediction number.

Source
The more formal formula is the following one.
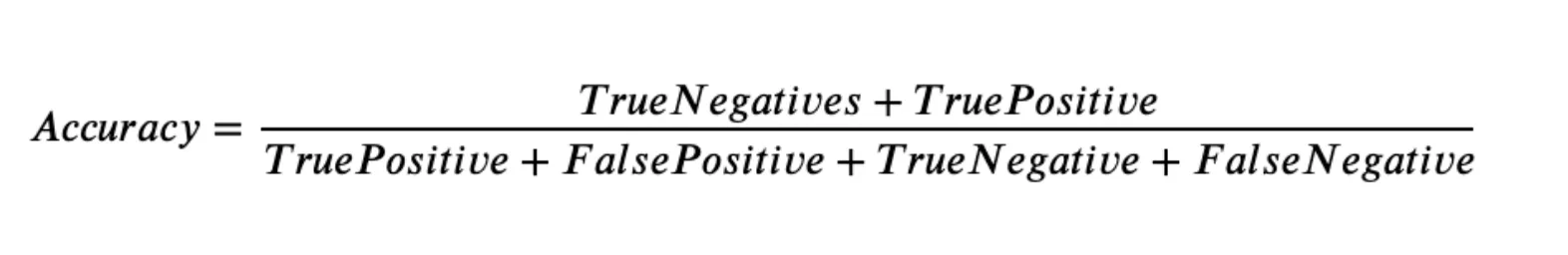
Source
So, the Hamming score algorithm for the binary Classification task is as follows:
Get predictions from your model;
Calculate the number of True Positives, True Negatives, False Positives, and False Negatives;
Use the Accuracy formula for the binary case;
And analyze the obtained value.
Yes, it is as simple as that. But what about the multiclass case? Well, there is no specific formula, so we suggest using the basic logic behind the metric to get the result. The Hamming score algorithm for the multiclass Classification task is as follows:
Get predictions from your model;
Calculate the number of correct predictions;
Divide it by the total prediction number;
And analyze the obtained value.
To back us up, we prepared a Google Colab notebook featuring calculating Accuracy and Hamming score for various tasks. Please look at it if you want proof that the Accuracy score and Hamming score are interchangeable for binary and multiclass cases.
Hamming score in a multi-label use case
However, Hamming score differs from the Accuracy in a multi-label use case. The difference is minimal, but it significantly impacts the metric making Hamming score a more viable metric for such tasks.
Let’s check out a simple example. Imagine having three classes and an object corresponding to class 1 and class 2 by ground truth. Your classifier predicts this sample as being of class 1 only. How do Accuracy and the Hamming score view such a situation?
Accuracy: This prediction is incorrect as the predicted classes are not fully equal to the ground-truth ones. The Accuracy score is 0;
Hamming score: We split the ground truth into two parts - one for class 1 and the other for class 2. In such a case, the algorithm got one part correct and failed on the other. The Hamming score for the prediction is 0.5.
When evaluating a multi-label task, the Hamming score will consider the partially correct predictions. The Hamming score algorithm for the multi-label Classification task is as follows:
Get predictions from your model;
Split the ground truth and predictions into parts;
Compare the corresponding pieces and calculate the number of correct predictions ;
Divide it by the total prediction number;
And analyze the obtained value.
Interpreting Hamming score
In the Hamming score case, the metric value interpretation is straightforward. If you get more correct predictions, it results in a higher Hamming score. The higher the measured value, the better. The best possible value is 1 (if a model got all the predictions right), and the worst is 0 (if a model did not make a single correct prediction).
From our experience, you should consider Hamming score > 0.9 as an excellent score,Hamming score > 0.7 as a good one, and any other score as the poor one. Still, you can set your own thresholds as your logic and task might vary highly from ours.
Just as Accuracy, the Hamming score has two massive drawbacks that must be considered when using it:
Imbalance problem;
Being uninformative.
Hamming score calculation example
Let’s say we have a binary Classification task. For example, you are trying to determine whether a cat or a dog is on an image. You have a model and want to evaluate its performance using Hamming score. You pass 15 pictures with a cat and 20 images with a dog to the model. From the given 15 cat images, the algorithm predicts 9 pictures as the dog ones, and from the 20 dog images - 6 pictures as the cat ones. Let’s build a Confusion matrix first (you can check the detailed calculation on the Confusion matrix page).
| Ground truth Cat | Ground truth Dog |
Predicted Cat | TP = 6 | FP = 6 |
Predicted Dog | FN = 9 | TN = 14 |
Excellent, now let’s calculate the Hamming score using the formula for the binary Classification task (the number of correct predictions is in the green cells of the table, and the number of the incorrect ones is in the red cells).
Hamming score = (TN + TP) / (TP + FP + TN + FN) = (14 + 6) / (6 + 6 + 14 + 9) ~ 0.57
Ok, great. Let’s expand the task and add another class, for example, the bird one. You pass 15 pictures with a cat, 20 images with a dog, and 12 pictures with a bird to the model. The predictions are as follows:
15 cat images: 9 dog pictures, 3 bird ones, and 15 - 9 - 3 = 3 cat images;
20 dog images: 6 cat pictures, 4 bird ones, and 20 - 6 - 4 = 10 dog images;
12 bird images: 4 dog pictures, 2 cat ones, and 12 - 4 - 2 = 6 bird images.
Let’s build the matrix.
| Ground truth Dog | Ground truth Bird | Ground truth Cat |
Predicted Dog | 10 | 4 | 9 |
Predicted Bird | 4 | 6 | 3 |
Predicted Cat | 6 | 2 | 3 |
Let’s use the basic logic behind the Hamming score metric to calculate the value for the multiclass case.
Number of correct predictions = 10 (dog) + 6 (bird) + 3 (cat) = 19;
Total number of predictions = 10 + 4 + 9 + 4 + 6 + 3 + 6 + 2 + 3 = 47;
Hamming score = 19 / 47 ~ 0.4
Finally, here is the Hamming score calculation example for a multi-label task. Here are the objects (a green cell means that an object corresponds to a specific class, whereas a red cell signalizes the opposite):
| Ground truth Class 1 | Ground truth Class 2 | Ground truth Class 3 |
Object 1 | 1 | 1 | 0 |
Object 2 | 1 | 1 | 0 |
Object 3 | 1 | 1 | 1 |
And here are the predictions:
| Predicted Class 1 | Predicted Class 2 | Predicted Class 3 |
Object 1 | 0 | 1 | 1 |
Object 2 | 1 | 1 | 0 |
Object 3 | 1 | 0 | 1 |
Let’s compare the ground truth and the predictions row by row.
Row 1: An algorithm got one class correct and two incorrect - 1 / 3
Row 2: An algorithm got all the classes correct - 1
Row 3: An algorithm got two classes correct and one incorrect - 2 / 3
Hamming score = (Row 1 + Row 2 + Row 3) / 3 = 2 / 3 ~ 0.66
Hamming score in Python
The Hamming score is not a popular Machine Learning metric in the Data Science community. First, it is similar to Accuracy in most cases. Second, Data Scientists do not solve that many multi-label tasks daily. This is why the significant Machine Learning libraries do not have the Hamming score implemented.
So, unfortunately, you can not simply use a scikit-learn (sklearn) Hamming score function to get a prediction as there is no such function. Still, if you really want to use the Hamming score, you can do some coding yourself or use one of the community’s implementations.
