Rprop

Most of the gradient based solvers use the magnitude and the sign of the gradient of the objective function. This heuristic often works well but there is no guarantee that this is always the good choice.

To see that is might work extremely badly, let us see the following examples,

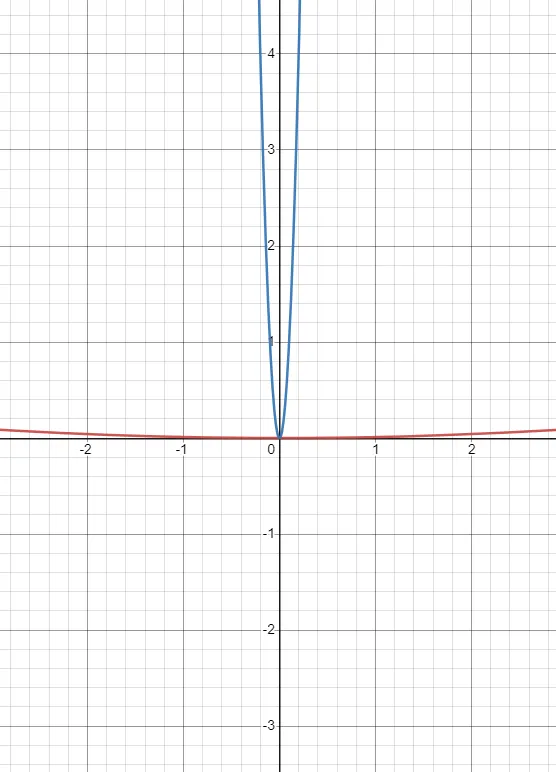
These functions have the same minima but the gradients are drastically different. The gradient for the blue curve explodes, while for the red, it vanishes.

To tackle this scenario, we can make use of the sign of the gradient, disregarding the magnitude.

Rprop uses the sign of the gradient to update the step-size for each of the weights.

If the first and second gradients have the same direction, we can be relatively sure that we are moving in the right direction then the step size for that particular weight can be increased multiplicatively by a factor that is greater than 1, (for example, 1.2).

If the gradients don't have the same sign, then the step-size should be decreased multiplicatively (e.g. by a factor 0.5).

Major Parameters

• Base Learning Rate
• Etas
• Step Sizes

Etas

They are the factors by which the step-size is scaled.

Step sizes

They define the maximum and minimum step size in the training process.

Code Implementation

      # importing the library
import torch
import torch.nn as nn

x = torch.randn(10, 3)
y = torch.randn(10, 2)

# Build a fully connected layer.
linear = nn.Linear(3, 2)

# Build MSE loss function and optimizer.
criterion = nn.MSELoss()

# Optimization method using Rprop
optimizer = torch.optim.Rprop(linear.parameters(), lr=0.01, etas=(0.5, 1.2),
 step_sizes=(1e-06, 50))

# Forward pass.
pred = linear(x)

# Compute loss.
loss = criterion(pred, y)
print('loss:', loss.item())

optimizer.step()