AMSgrad Variant (Adam)
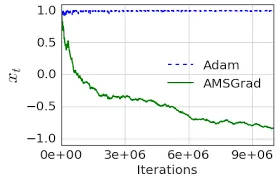
While the Adam optimizer, which made use of momentum as well as the RMS prop, was efficient in adjusting the learning rates and finding the optimal solution, we have found that certain convergence issues with it. Research has been able to show that there are simple one dimensional convex functions for which the Adam is not able to converge.
Adam makes use of adaptive gradient and updates the parameters separately. The updates might increase or decrease depending upon the calculated exponential moving average of the gradients. But sometimes, the updates of the the parameters is large which doesn't result in convergence. Citing the paper "On The Convergence of ADAM and beyond",
The key difference between AMSGRAD and ADAM is that it maintains the maximum of all until the present time step and uses this maximum value for normalizing the running average of the gradient instead of in ADAM
Hence, the difference between the AMSgrad and Adam is the calculated second moment vector which is used to update the parameters. To put it simply, AMSgrad uses the maximum second moment up until the iteration to update the parameters.
Performance of ADAM and AMSgrad has been presented on a synthetic function to outline the convergence problem of the ADAM. Source