Intersection over Union (IoU)
If you have ever worked on an Object Detection, Instance Segmentation, or Semantic Segmentation tasks, you might have heard of the popular Intersection over Union (IoU) Machine Learning metric. On this page, we will:
- Сover the logic behind the metric;
- Explain why do we need IoU;
- Check out the metric’s formula;
- Find out how to interpret the metric value;
- Calculate IoU on a simple example;
- And see how to work with the Intersection over Union using Python.
Let’s jump in.
What is Intersection over Union?
In general, Deep Learning algorithms combine Classification and Regression tasks in various ways. For example, in the Object Detection task, you need to predict a bounding box (Regression) and a class inside the bounding box (Classification). In real life, it might be challenging to evaluate all at once (mean Average Precision can help you with that), so there are separate metrics for the Regression and Classification parts of the task. This is where Intersection over Union comes into the mix.
To define the term, in Machine Learning, IoU means Intersection over Union - a metric used to evaluate Deep Learning algorithms by estimating how well a predicted mask or bounding box matches the ground truth data. Additionally, for your information, IoU is referred to as the Jaccard index or Jaccard similarity coefficient in some academic papers.
So, to evaluate a model using the IoU metric, you need to have:
- The ground truth annotation (either masks or bounding boxes);
- And the model’s predictions of a similar type as the ground truth ones.
Intersection over Union formula
Fortunately, Intersection over Union is a highly intuitive metric, so you should not experience any challenges in understanding it. IoU is calculated by dividing the overlap between the predicted and ground truth annotation by the union of these.
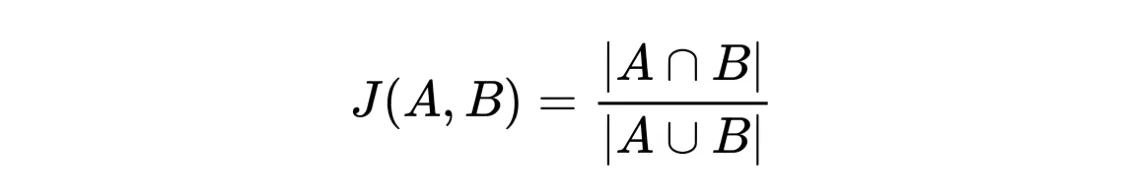
Source
It is not a problem if you are unfamiliar with the mathematical notation because the Intersection over Union formula can be easily visualized.
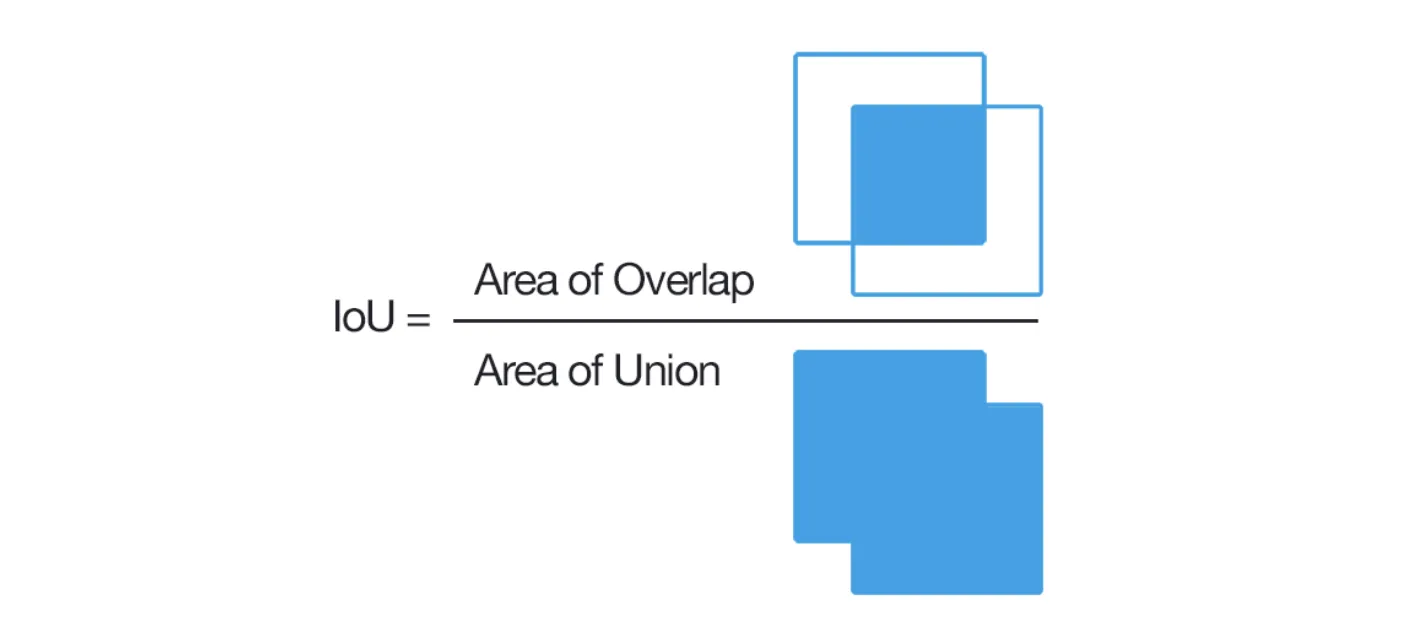
Source
You might be wondering why we are calculating some overlap/union area, not the (x, y) pairs straightaway. In a real-life scenario, it is highly unlikely that the predicted coordinates will exactly match the ground truth ones for various reasons (basically, the model’s parameters). Still, we need a metric to evaluate the bounding boxes (and masks), so it seems reasonable to reward the model for the predictions that heavily overlap with the ground truth.
So, the Intersection over Union algorithm is as follows:
- Get a prediction from your model;
- Compare the predicted bounding box (or mask) with the ground truth one;
- Calculate the area of overlap and the area of union between these;
- Divide the overlap between the annotations by their union;
- Analyze the obtained value;
- Repeat steps 1-5 for every test image;
- Take the mathematical average of the IoU scores to get the final result over your test set.
Intersection over Union for multiple objects
With the basic Intersection over Union algorithm in place, it is time to hit the potential case of dealing with multiple objects.
Fortunately, the solution is straightforward. There is no need to reinvent the wheel and come up with some unified IoU value for all the objects. The most effective way to solve such a case is by applying the IoU metric to each object individually.
Interpreting Intersection over Union
In the IoU case, the metric value interpretation is straightforward. The bigger the overlapping, the higher the score, the better the result.

Source
The best possible value is 1. Still, from our experience, it is highly unlikely you will be able to reach such a score.
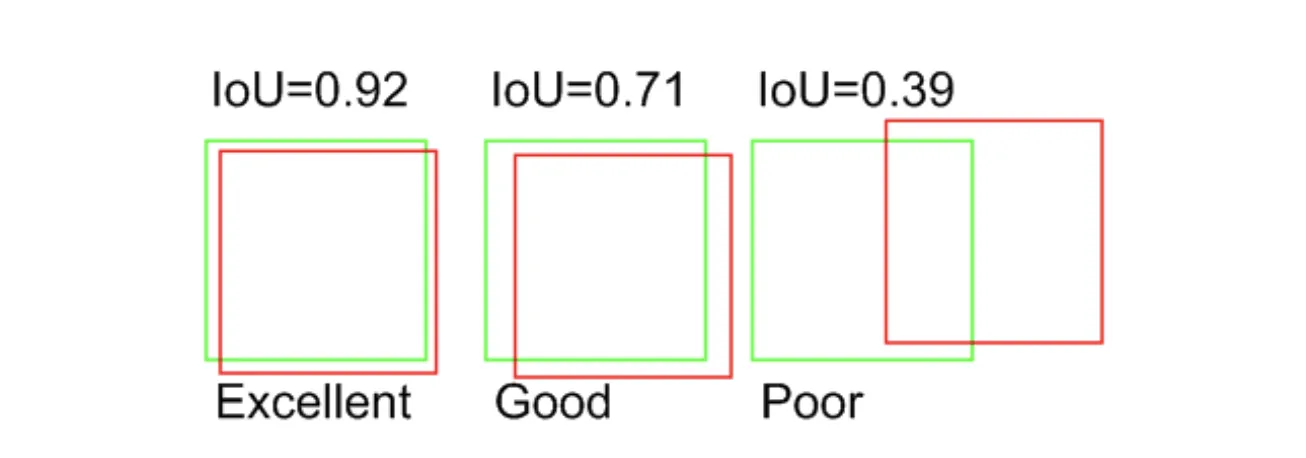
Source
Our suggestion is to consider IoU > 0.95 as an excellent score, IoU > 0.7 as a good one, and any other score as the poor one. Still, you can set your own thresholds as your logic and task might vary highly from ours.
Intersection over Union calculation example
Let’s say that we have two bounding boxes with the coordinates as presented in the image below.
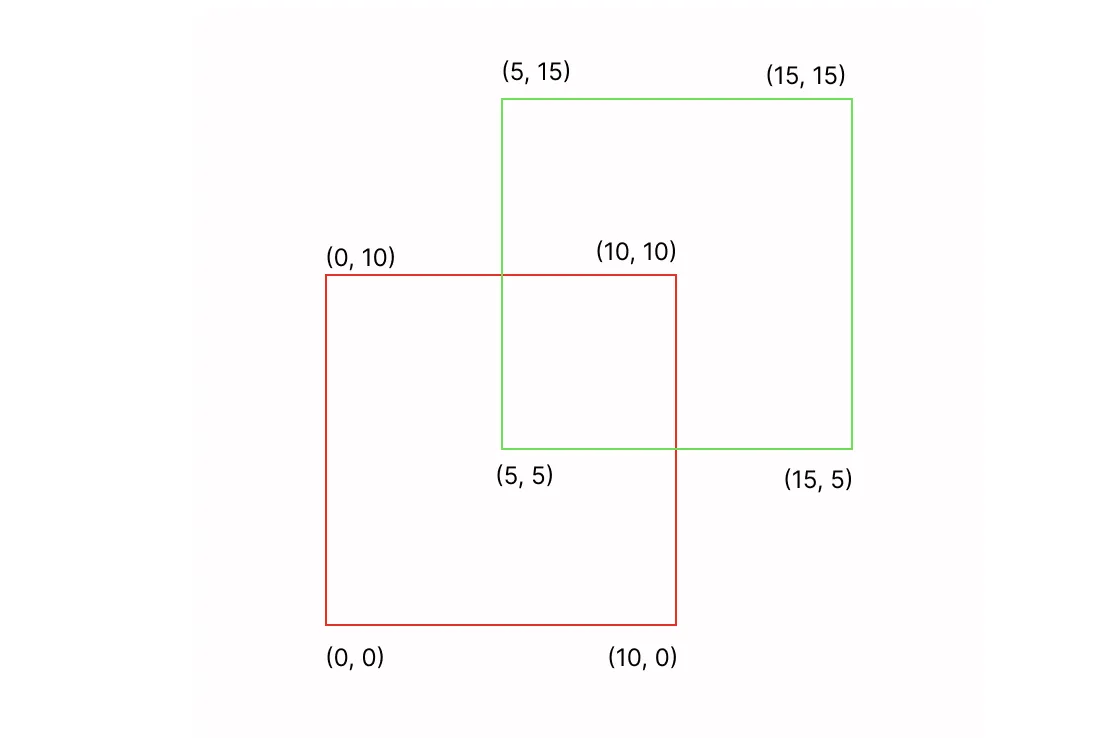
In such a case:
- Area of Overlap: 5 * 5 = 25;
- Area of Union: Area of the Red Bounding Box + Area of the Green Bounding Box - Area of Overlap = 10 10 + 10 10 - 25 = 175
- IoU: Area of Overlap / Area of Union = 25 / 175 ~ 0.14 - poor IoU
Intersection over Union in Python
Intersection over Union is widely used in the industry (especially for the Deep Learning tasks), so all the Deep Learning frameworks have their own implementation of this metric. Moreover, IoU is relatively simple in its concept, so you can manually code it without any issues. For this page, we prepared two code blocks featuring using Intersection over Union in Python. In detail, you can check out:
- Intersection over Union in NumPy;
- Intersection over Union in PyTorch.
Intersection over Union in NumPy
Intersection over Union in PyTorch
Learn more about the related vision AI model families
P.S. Generalized Intersection over Union (GIoU) metric
Also, there is the Generalized Intersection over Union (GIoU) metric built on top of the original IoU. It is less popular as it is often used to evaluate underperforming models. In short, the value of Generalized IoU increases as the predicted mask or bounding box moves towards the ground truth giving Data Scientists the feeling that their experiments are successful and moving in the right direction. Please refer to the original post to learn more about the GIoU.
